Линеарни зависни и независни редови: дефиниција, примери

Во оваа публикација, ќе разгледаме што е линеарна комбинација на жици, линеарно зависни и независни жици. Ќе дадеме и примери за подобро разбирање на теоретскиот материјал.

Дефинирање на линеарна комбинација на жици

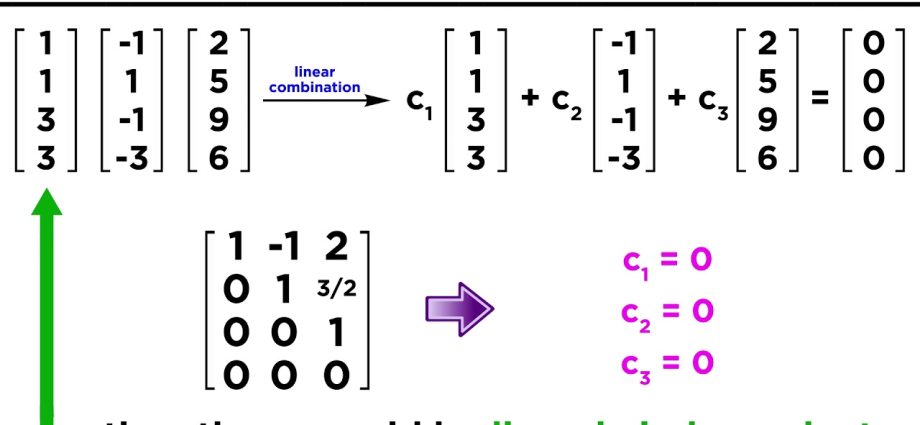
Линеарна комбинација (LK) термин s₁со₂, …, с_n матрица A наречен израз од следнава форма:

αs₁ + αs₂ + … + αs_n

Ако сите коефициенти α_i се еднакви на нула, значи LC е тривијални. Со други зборови, тривијалната линеарна комбинација е еднаква на нултата редица.

На пример: 0 · с₁ + 0 · s₂ + 0 · s₃

Според тоа, ако барем еден од коефициентите α_i не е еднаква на нула, тогаш LC е нетривијални.

На пример: 0 · с₁ + 2 · s₂ + 0 · s₃

Линеарно зависни и независни редови

Системот на жици е линеарно зависни (LZ) ако постои нетривијална линеарна комбинација од нив, која е еднаква на нултата линија.

Оттука произлегува дека нетривијалниот LC во некои случаи може да биде еднаков на нултата низа.

Системот на жици е линеарно независни (LNZ) ако само тривијалната LC е еднаква на нултата низа.

Забелешки:

• Во квадратна матрица, системот на редови е LZ само ако детерминантата на оваа матрица е нула (на = 0).
• Во квадратна матрица, системот на редови е LIS само ако детерминантата на оваа матрица не е еднаква на нула (на ≠ 0).

Пример за проблем

Ајде да дознаеме дали системот на жици е {s₁ = {3 4};s₂ = {9 12}} линеарно зависни.

Одлука:

1. Прво, да направиме LC.

α₁{3 4} + a₂{9 12}.

2. Сега да дознаеме кои вредности треба да ги земеме α₁ и α₂така што линеарната комбинација е еднаква на нула низа.

α₁{3 4} + a₂{9 12} = {0 0}.

3. Да направиме систем од равенки:

4. Првата равенка поделете ја со три, втората со четири:

5. Решението на овој систем е кое било α₁ и α₂, Со α₁ = -3а₂.

На пример, ако α₂ = 2потоа α₁ =-6. Ги заменуваме овие вредности во системот на равенки погоре и добиваме:

Одговор: па линиите s₁ и s₂ линеарно зависни.